8 sinif teog matematİk trİgonometrİ konusu ve ÜÇgenlerİnİn oran ve kurallari (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni üçgeni kenar uzunlukları bulma 30 derecenin karşısındaki kenarın uzunluğu hipotenüs uzunluğunun yarısına eşit olur60 derecenin karşısındaki kenarın uzunluğu ise hipotenüsün yarısı alınıp birde kök 3 ile çarpılarak bulunur Örnek üçgeni (

5 Soru 30 60 90 Ucgeni Youtube
30 60 90 üçgeni özelliği
30 60 90 üçgeni özelliği-(30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ 3 olur 6 (15° 75° 90°) Üçgeni 30 60 90 üçgeni olarak geçen bu kural hakkında öğrenciler kafasında birçok soru bulunmaktadır 30 60 90 üçgeninin kuralı nedir, özellikleri nelerdir gibi sorular öğrencilerin merak




30 60 90 Ucgeni
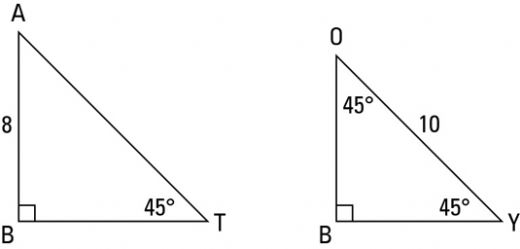
90 nin karşısında 2 katı olurA) 2 2 B) 2 3 C) 3 2 D) 4 2 E) 6 Çözüm wwwmatematikkolaynet Üçgeni dışardan 45 45 90 üçgeni olacak şekilde uzatalım Büyük üçgen 30 60 90 üçgeni olur 90 'nin karşısında 6 2 var sa 30 nin karşısında yarısı olur 6 2 3 2 dir 2 45 45 90 üçgeninde 45 nin karşısında 3 2 var sa; Üçgeni üçgeninde Hipotenüs, 90° nin karşısındaki sayıdır Hipotenüsü gören açı en büyük açı olduğu için onu gören kenar da en büyük kenardır üçgeni geometri konusunda en çok karşınıza çıkan ve her üçgende kullanabileceğiniz bir kombinasyondur üçgeni diğer üçgen
30 60 90 üçgeni Geometrinin açılar konusunun belirli kurallara bağlı olan özel üçgenlerinden birisidir 30 60 90 üçgeni özelliklerinin bilinmesi geometrinin temel kurallarındandır Geometri dersi bir bisikletin zinciri gibidir Dişlisinden birisi dahi çıkan bisiklet zinciri tamamen işlevini yitirdiği gibi geometri de öyledir The and Triangles Posted on 12 March 13 by RobertLovesPi It is wellknown that an altitude splits an equilateral triangle into two triangles, and that a diagonal splits a square into two triangles The properties of these "special right triangles," as they are often called, are wellunderstood, andDİK VE ÖZEL ÜÇGENLER TEST2 ÇÖZÜMLERİ Çözüm ABC üçgeninde (30 60 90) hipotenüs uzunluğuna 2 br dersek 30° nin karşısındaki kenar 1 br dirABC üçgeni ikizkenar (45 45 90) olur ki α45°=60° olacağından α=15° bulunur
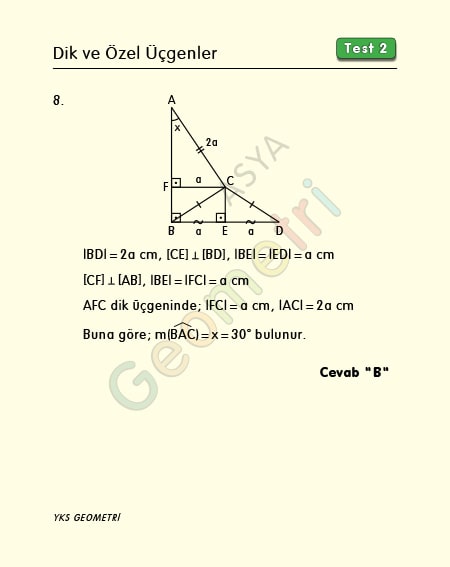
ABE üçgeni (45 45 90 ) üçgeni ve AEC üçgeni (30 60 90 ) üçgeni olur ABE üçgeninde, dik kenar hipotenüsün yarısının 2 katı olduğundan AE = 4 2br dir AEC üçgeninde hipotenüs 30 nin karşısındaki dik kenarın iki katı olduğundan AC = 8 2br olur Cevap B'dir 30 60 90 üçgeni kuralı bir dik üçgen üzerinden ele alınan sabit bir üçgendir 30 derecenin karşısında olan kenar hipotenüs uzunluğunun yarısına verir 60 derecenin karşısında olan kenar ise, 30 derecenin gördüğü kenar üzerinden kök 3 ile çarpılır Aynı şekilde 90 derecenin karşısında olan kenar ise, 30 derecenin 45 45 90 üçgeni ile 30 60 90 üçgeni arasında ilişki kurmak için bazı sorularda bu iki üçgen iç içe verilebilir Yukarıdaki örnekte olduğu gibi bu tür sorularda bazen çizim yöntemini kullanarak iki üçgeni elde etmemiz gerekir




30 60 90 Ucgeni Akilli Geometri



Teog Trigonometri Ozel Ucgenler Konu Anlatim Video Ozancorumlu Com Turkiye Nin Egitim Sitesi
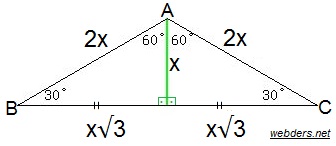
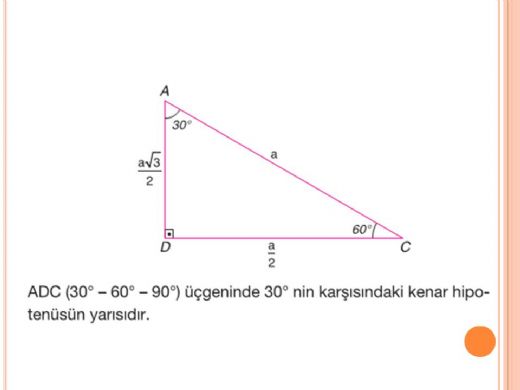
30 60 90 üçgeni 37 53 90 üçgeni 45 45 90 üçgeni 1 1 atalante #7593 2108 ~ 803 22,5 67,5 90 üçgeni oldum olası kim bulmuş diye merak ettiğim üçgendir lakin çözümü oldukça basittir 67,5 olan açıyı 22,545 olarak ayırırsınız, bir tarafta ikizkenar üçgen, diğer tarafta ise 45 45 90 30 30 1 üçgeni 30 30 1 üçgeni bir ikizkenar üçgendir 1 derecelik açının karşısından karşı kenara dikme indirdiğinizde iki tane eş 30 60 90 üçgeni elde ederiz Yamuk sorularında Yamuk sorularında dikme indirdiğimiz zaman 30 60 90 üçgeni karşımıza çok çıkmaktadırYine aynı oranlarla kenarları bulmak ve alan hesaplamak kolay olacaktır(30° – 60° – 90°) Üçgeni ABC eşkenar üçgeni yükseklikle ikiye bölündüğünde ABC eşkenar üçgeni yükseklikle ikiye bölündüğünde ABH ve ACH (30° 60° 90°) üçgenleri elde edilir



The Easy Guide To The 30 60 90 Triangle



1
B açısındaki 67,5 dereceyi 45 ve 22,5 şeklinde ayırırsak iki tane ikiz kanar üçgen oluştururuz (birisi ikiz kenar dik üçgen) 45 derecelerin karşına x desek 90 nın karşısı xkök2 olur (taban açıları 22,5 olan ikiz kenar üçgenden)diğer tarafta xkök2 olurBu dikmenin sağ tarafına geçelim burda bir 90 60 30 üçgeniBu yazımızda 30 60 90 Üçgeni, 45 45 90 Üçgeni, 30 30 1 Üçgeni, 15 75 90 Üçgeni, Üçgende İç Açılar Toplamı, Dış Açılar Toplamı, Roket Kuralı ve çok daha fazlası hakkında bilmen gerekenler ile Üçgende Açılar konusuna ait soruları çözerken işine yarayacağını düşündüğümüz ipuçları yer alıyor Umarız15 75 90 üçgeni 30 60 90 üçgeni 37 53 90 üçgeniBCaa2a3(30,60,90) dik üçgeni(300,600,900) üçgeninde 300lik açının karşısındaki kenarın uzunluğu hipotenüsün yarısına, 600lik açının karşısındaki kenarın uzunluğu ise hipotenüsün yarısının katına eşittir yada 300lik açının katı diyebilirizÖrnekAACABC dik üçgeninde c açısının ölçüsü



A 1 6m Tall Person Stands Right Beneath The Bulb Fitted At The Ceiling Of The Room And Therefore Makes No Shadow She Moves 2 Meters To Make The Length Of Her Shadow




30 30 1 Ucgeni Not Bu
(30 60 90) Üçgeni (30 60 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz Öğretmenlerinizin 'şuradan bir dikme indir', 'buradan bir çizgi çek' dediği yerler aslında üçgeni bulmanız içindir 30 60 90, 45 45 90, 30 30 1 gibi bir tane de 15 75 90 üçgeni vardır Gelin 15 75 90 üçgeni özellikleri nasılmış, hep birlikte öğrenelimGeometri konuları dik üçgenler, özel üçgenler, 30 60 90 üçgeni, 45 45 90 üçgeni, 15 75 90 üçgeni, 15 30 135 üçgeni, öklid, pisagor, muhteşem üçlü, kenarlarına ve açılarına göre özel üçgen soruları Görselleri inceleyebilir, sayfa sonundan PDF formatındaki 11 Sınıf dik ve özel üçgenler test1 dosyasını
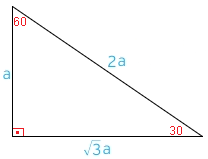



30 60 90 Ucgeni Webders Net
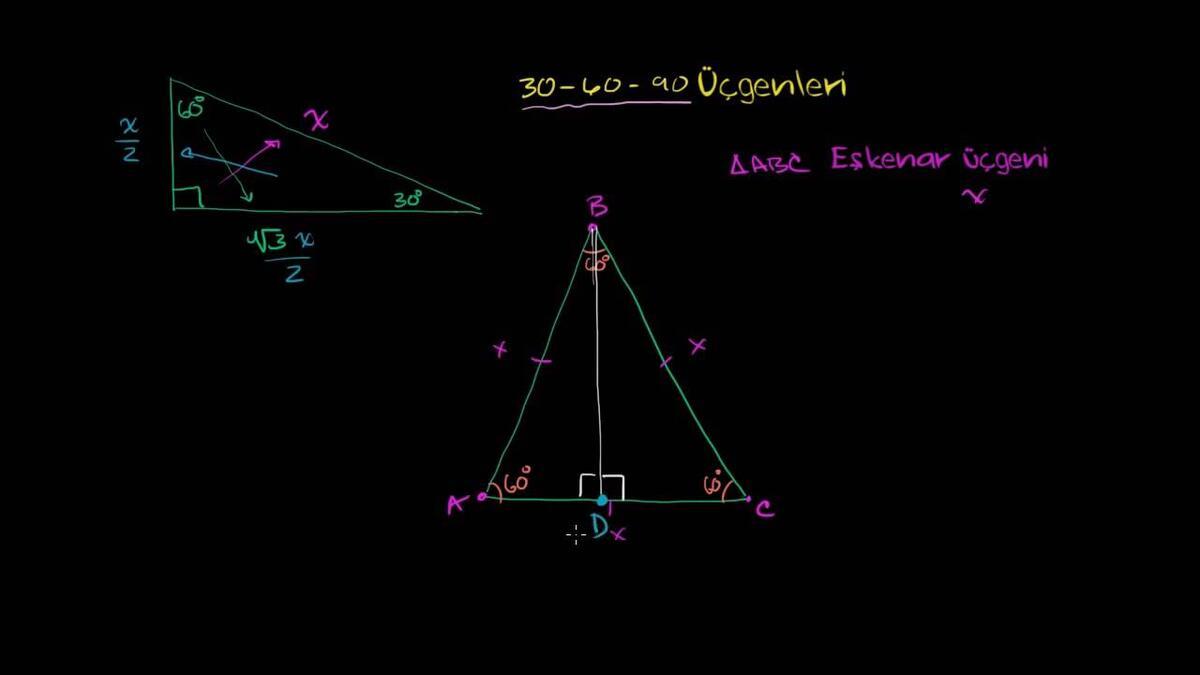



30 60 90 Ucgeni Kurali Nedir 30 60 90 Ucgeninin Ozellikleri Nelerdir Egitim Haberleri
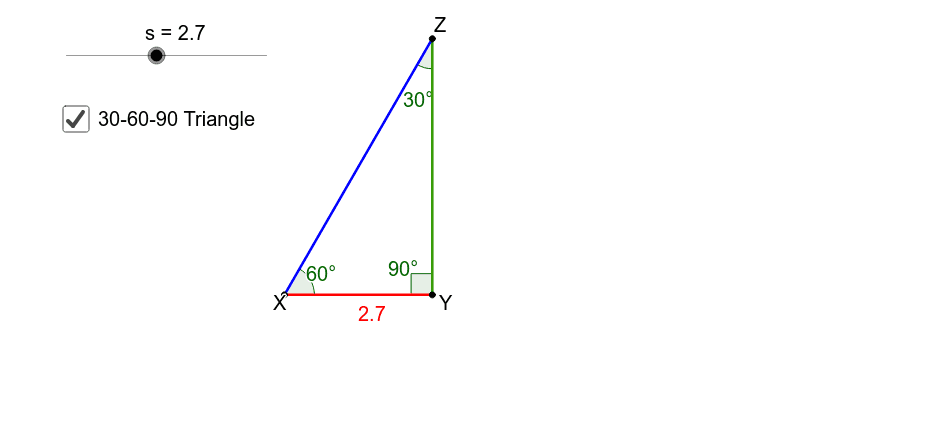
Üçgeni Bir dik üçgende dar açılardan biri 30 ise, 30 derecelik açının karşısındaki kenar hipotenüsün yarısında eşittir 60 derecelik açının karşısındaki kenarın uzunluğu da 30 derecelik açı karşısındaki kenarın katına eşittirÜçgeni Kenar Oranları İspatı Geri Üçgeni Kenar Oranları İspatı KhanAcademyTurkce 509K subscribers Subscribe Özel dik üçgeni veya 30 60 90 üçgenini çözmek için formüller basittir Kısa bacak, uzun bacak veya hipotenüs biliyorsanız tüm ölçüleri kolayca bulabilirsiniz!



90 60 30 Ucgeni




Trigonometry Act Math
A) 3 B) 4 C) 4 2 D) 4 3 E) 7 Çözüm wwwmatematikkolaynet ABC üçgeni 30 60 90 üçgenidir Bu üçgende 30 nin karşısı hipotenüsün yarısıdır Bu sebeple; 30 60 90 Üçgeni 15 75 90 Üçgeni Özelliği Bu makaledeki notlar 15 75 90 üçgeninin özelliği 30 Özel Üçgenler DİK ÜÇGEN Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir 30 60 90 üçgeni zaten geometride en çok kullandığımız özel üçgendir 1 30 30 üçgenine en çok rastladığımız soru tipi düzgün altıgen ile ilgili olandır Düzgün altıgende arada bir boşluk olacak şekilde iki köşegeni birleştirdiğimizde ortaya 30 30 1 üçgeni çıkmaktadır




30 60 90 Ucgeni Kurali Nedir 30 60 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Son Dakika Egitim Haberleri




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz
Buna geometri dersinde muhteşem üçlü denir ÜçgeniBir dik üçgende dar açılardan biri 30 ise, 30 derecelik açının karşısındaki kenar hipotenüsün yarısına eşittir Üçgeni60 derecelik açının karşısındaki kenarın uzunluğu da 30 derecelik açı karşısındaki kenarın katına eşittirÖklid Teoremi30 – 60 – 90 Üçgeni 45 – 45 – 90 Üçgeni 30 – 1 – 30 Üçgeni 15 – 75 – 90 Üçgeni Örnek1 Aşağıdaki ABC dik üçgeninde AB = 5 cm AC = 4 cm 30 60 90 üçgeni 17 Temmuz 18 by ibrahimhocca, posted in Genel 30 60 90 üçgeni 30 60 90 üçgeni çoğu soruda karşımıza gelir o nedenle bu üçgenin özelliklerini iyi bilmek gerekir Olay çok basit öncelikle dik üçgeni tanıyalım Dik üçgen olması için zaten üçgenin açılarından biri 90 derece olmalı Önce bu 90
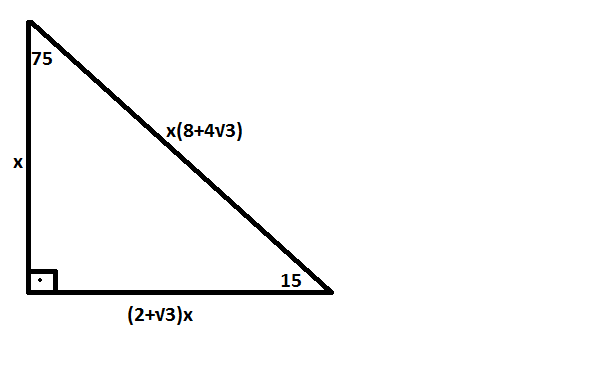



15 75 90 Ucgeni Uludag Sozluk




Special Right Triangles Sine Cosine Tangent Flashcards Quizlet
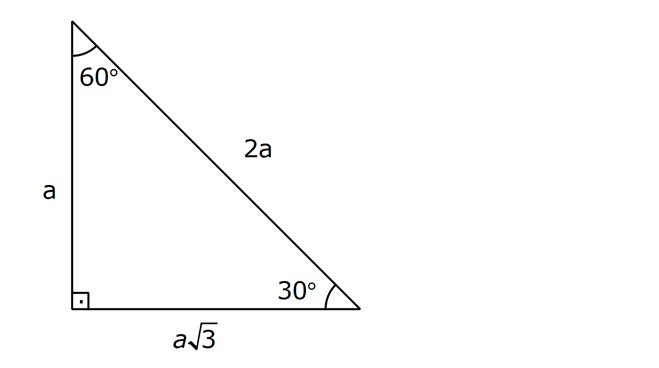
üçgeni üçgeni ve ispatı Açıları olan bir dik üçgende hipotenüs, 30°'nin karşısındaki kenar ve 60°'nin karşısındaki kenar arasında sırasıyla aşağıdaki oran vardır90 60 30 üçgeni kpss konu anlatımı üçgeni Açıları olan bir dik üçgende hipotenüs, 30°'nin karşısındaki kenar ve 60°'nin karşısındaki kenar arasında sırasıyla aşağıdaki oran vardır 30°'nin karşısındaki kenarın katıdır




If Tan Theta 21 Show That Cosec 2 Theta Sec 2 The



The Easy Guide To The 30 60 90 Triangle
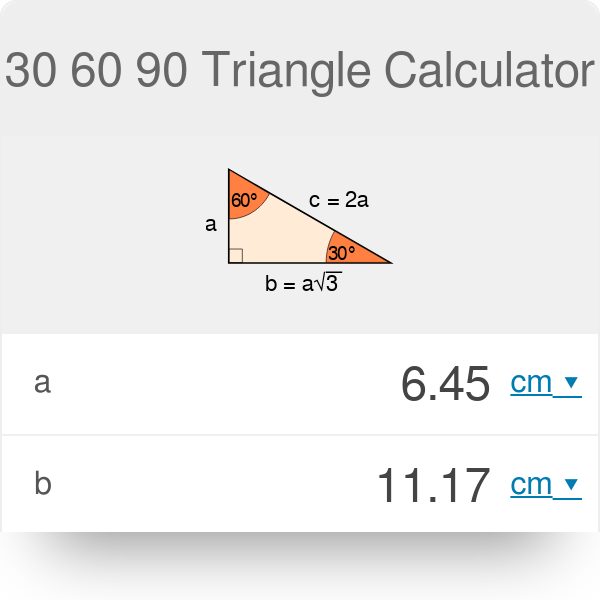
30 60 90 üçgeni özel üçgenler içerisinde belki karşımıza en çok çıkan üçgendir Bir öğrenci neyi çok iyi bilirsem sırtım yere gelmez diye sorarsa bunun cevabı da sanırım 30 60 90 üçgeni olacaktır Çünkü geometrinin temelini üçgenler oluşturmaktadır Geometride karşımıza çıkan özel dik üçgenler bulunmaktadır Bu özel dik üçgenlerden bir tanesi ise 30 60 90 üçgenidir Bu 30 60 90 üçgeni bir eş üçgenin yükseklik ile iki eş parçaya bölünmesinden oluşmuştur Bu üçgenin açıları 30 derece 60 derece ve 90 derecedir Bu açıları gören kenarların uzunluklarının ise belirli bir kuralı bulunmaktadır 30 derecelikDaha kısa bacak uzunluğu a'yı biliyorsak, şunu bulabiliriz b = a√3 c = 2a Daha uzun bacak uzunluğu b verilen bir parametre ise, o zaman a = b√3/3 c = 2b√3/3




Dik Ucgen Konu Detayi Webders Net




Index Of Wp Content Uploads 17 10
45 45 90 üçgeni ile 30 60 90 üçgeni arasında ilişki kurmak için bazı sorularda bu iki üçgen iç içe verilebilir Yukarıdaki örnekte olduğu gibi bu tür sorularda bazen çizim yöntemini kullanarak iki üçgeni elde etmemiz gerekirüçgeni özellikle üçgen içerisindeki hem açı hem de kenarı bulma konusunda büyük kolaylık sağlar Aynı zamanda özellikle herhangi bir geometrik şekil doğrusunda, ortaya çıkarılan üçgeni üzerinden alan kolayca bulunabilir Aynı zamanda analitik geometri üzerinde de birçok farklı işlem yapma imkanı8 AB 4 cm dir 2 60 nin karşısı, 30 nin karşısının 3 katıdır x 4 3 cm buluruz 55




30 60 90 Ucgeni Ve Ozellikleri Not Bu
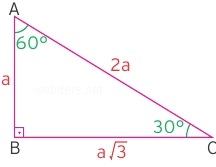



En Hizli 30 60 90 Ucgen Kenarlari
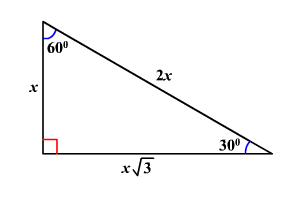
30 60 90 Üçgeni, Geometride özel üçgenler başlığı altında dik üçgenler konusu içerisinde incelenir Geometrik cisimlerden biri olan üçgenlerin 3 adet kenarı vardır Açıları ise 3 adet iç ve 3 adet dış açı olmak üzere 6 adettir Üçgenin iç açılarının toplamı üçgeni içerisinde açılara bakmak suretiyle kenar uzunluklarının hesaplaması kolayca yapılabilmektedir Bu doğrultuda 30 derecenin karşısındaki kenar a olursa, 60 derecenin karşısındaki kenar ise a kök 3 olarak ifade edilir 90 derecenin karşısındaki kenar ise 2a olarak öne çıkar 30 – 60 – 90 ÜÇgenİ Eşkenar üçgende bir kenara ait yükseklik çizilirse oluşan iki dik üçgenin de açıları 30° – 60° – 90° olur Bu eşkenar üçgenin bir kenarının uzunluğunu 2a kabul edersek, oluşan dik üçgenlerde 30 derecelik açının karşısı a




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz




30 60 90 Ucgeni Ibrahim Hocca
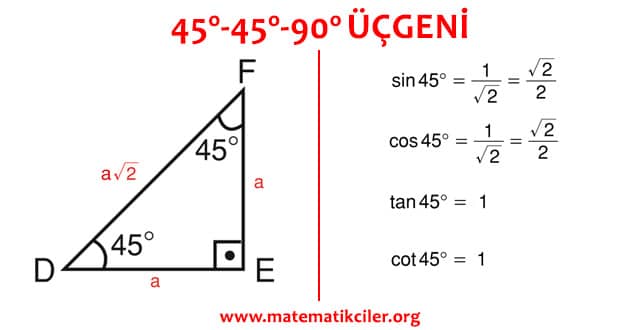
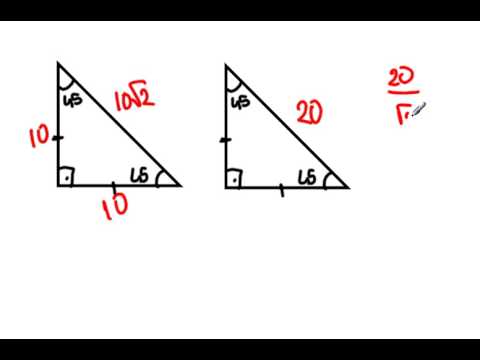
45 45 90 Üçgeni, özel üçgenlerden biri olup, geometri dersinde çok önemli bir yeri bulunmaktadır Trigonometrik bağıntıları çok iyi idrak etmek için 45 45 90 üçgenini çok iyi bilmek gerekirBu nedenle, bu üçgeni çok iyi bilmek karşılaşılacak tüm üçgeni – Matematik, Geometri ve Türkçe Bloğu (DGS, ALES, KPSS) Geometri Ara 12,14Üçgeni Kenar Oranları İspatı Üçgeni Kenar Oranları Üçgeni ile İlgili Soru Düzgün Altıgenin Alanı Özel Dik Üçgenler Tekrar Şu anda seçili olan öge bu Sonraki ders Trigonometrik Oranlar Sıralama ölçütü En çok oylanan




30 60 90 Ucgeni




180 Geometry Ideas In 21 Teaching Math Math Geometry Education Math
30 60 90 üçgeni Geometrinin açılar konusunun belirli kurallara bağlı olan özel üçgenlerinden birisidir 30 60 90 üçgeni özelliklerinin bilinmesi geometrinin temel kurallarındandır Geometri dersi bir bisikletin zinciri gibidir Dişlisinden birisi dahi çıkan bisiklet zinciri tamamen işlevini yitirdiği gibi geometri de öyledir(30 60 90) Üçgeni (30 30 1) Üçgeni Eşkenar Üçgen (30 30 1) Üçgeni (30 30 1) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz Sizi ve arkadaşlarınızı sitemize bekliyoruz )Orijinal video Sal Khan tarafından hazırlanmıştır Özel Dik Üçgenler Üçgenleri Üçgenleri Şu anda seçili olan öge bu Üçgeni




5 Soru 30 60 90 Ucgeni Youtube




30 60 90 Ucgeni Matematik Geometri Ve Turkce Blogu Dgs Ales Kpss



2




En Hizli 30 60 90 Ucgeni Ozellikleri



45 45 90 Ucgeni Matematikce




30 60 90 Ucgeni Turleri Ve Ozellikleri
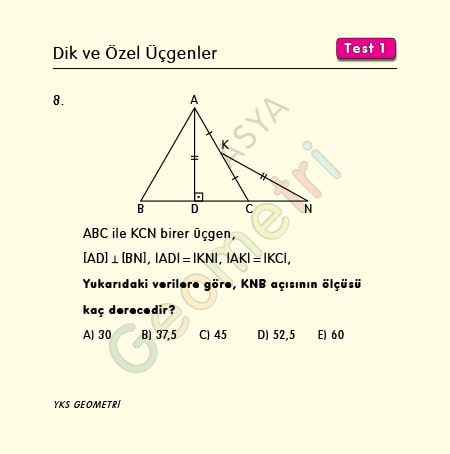



Vertical And Special Triangles Test 1




30 60 90 Ucgeni Ispat Youtube




30 60 90 Ucgeni Pow Bylge
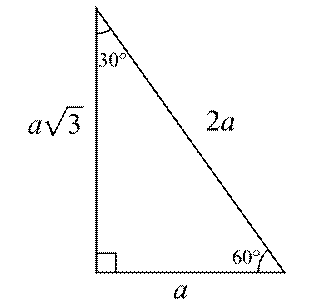



Dik Ucgende Trigonometrik Oranlar



6676 On Vimeo




Index Of Wp Content Uploads 18 05
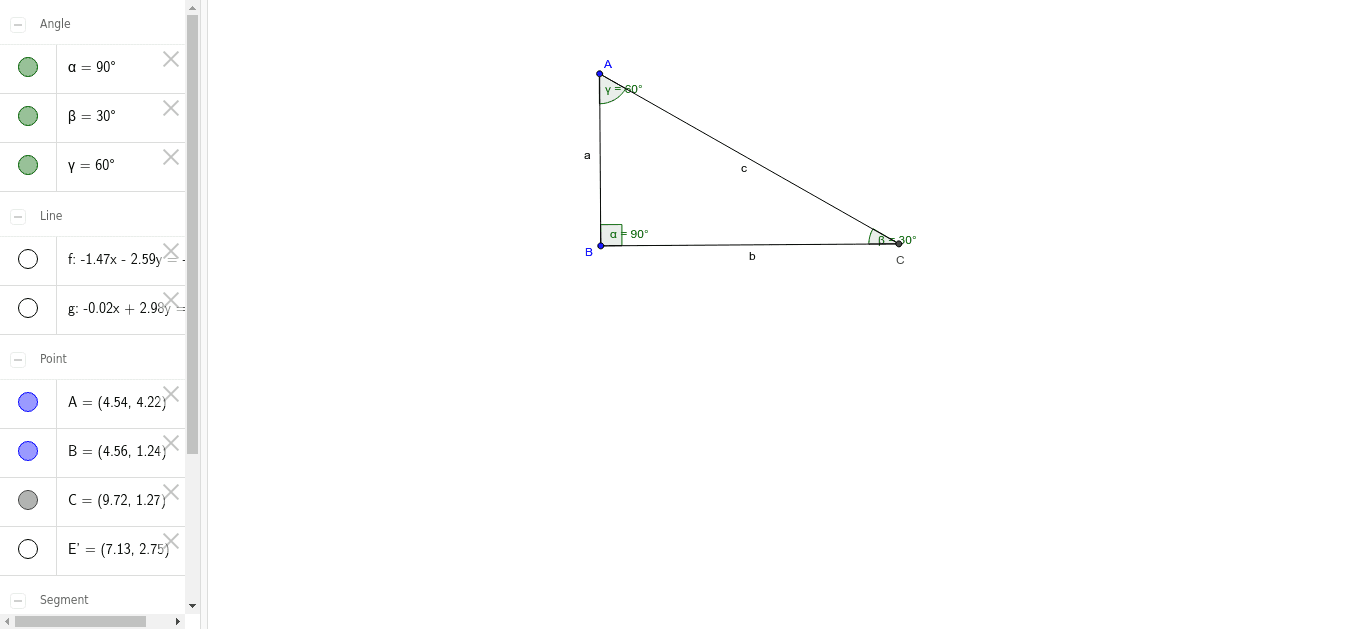



Triangle 30 60 90 Geogebra




3 The Following Diagram Shows A 45 45 90 Triangle Chegg Com




Special Right Triangles Sine Cosine Tangent Flashcards Quizlet




45 45 90 Ucgeni
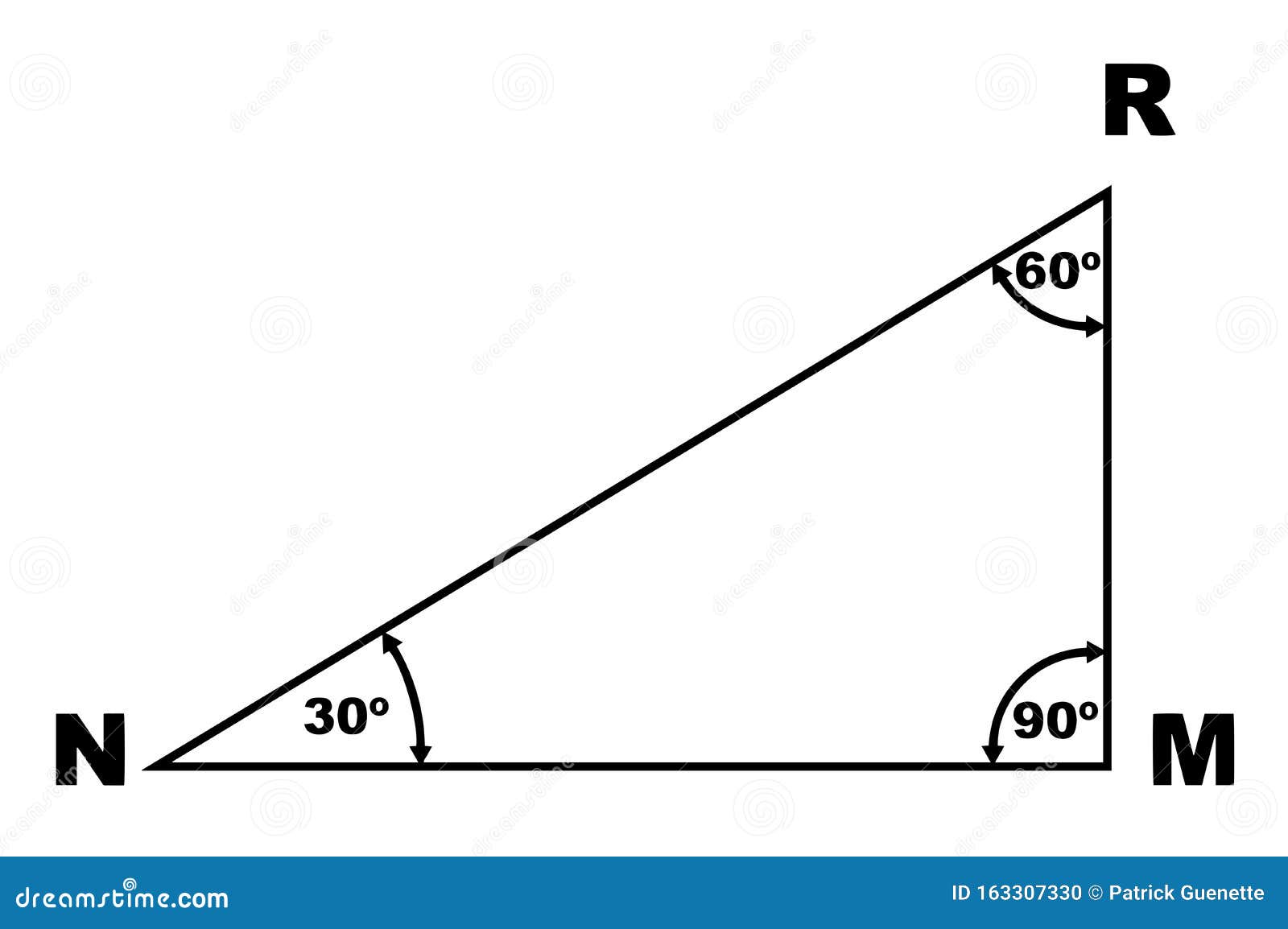



Triangle Degrees Stock Illustrations 248 Triangle Degrees Stock Illustrations Vectors Clipart Dreamstime



45 45 90 Ucgeni Matematikce




30 60 90 Ucgeni Nedir Ozellikleri Nelerdir Nasil Hesaplanir En Son Haberler Milliyet



1 30 30 Ucgeni Webders Net
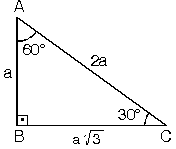



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir



Trigonometri Dik Ucgenlerdeki Trigonometrik Oranlar Matematikciler Com




30 60 90 Triangle Calculator Formula Rules




30 60 90 Ucgeni Youtube



Special Right Triangles 30 60 90 Geogebra
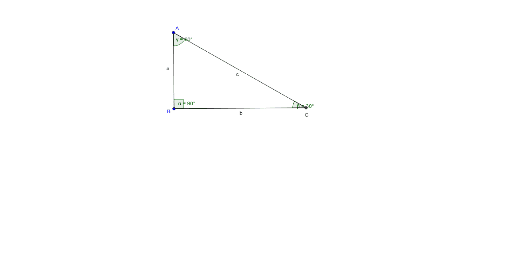



Triangle 30 60 90 Geogebra
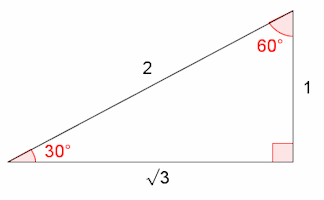



Common Trigonometric Ratios




Triangle Degrees Stock Illustrations 248 Triangle Degrees Stock Illustrations Vectors Clipart Dreamstime



2
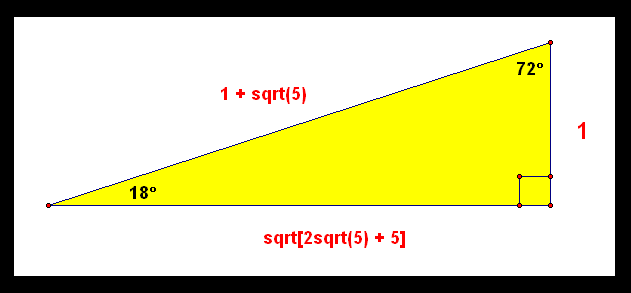



The 9 81 90 Triangle Robertlovespi Net




How Do You Solve The Right Triangle Given The Hypotenuse Is 4 And



2
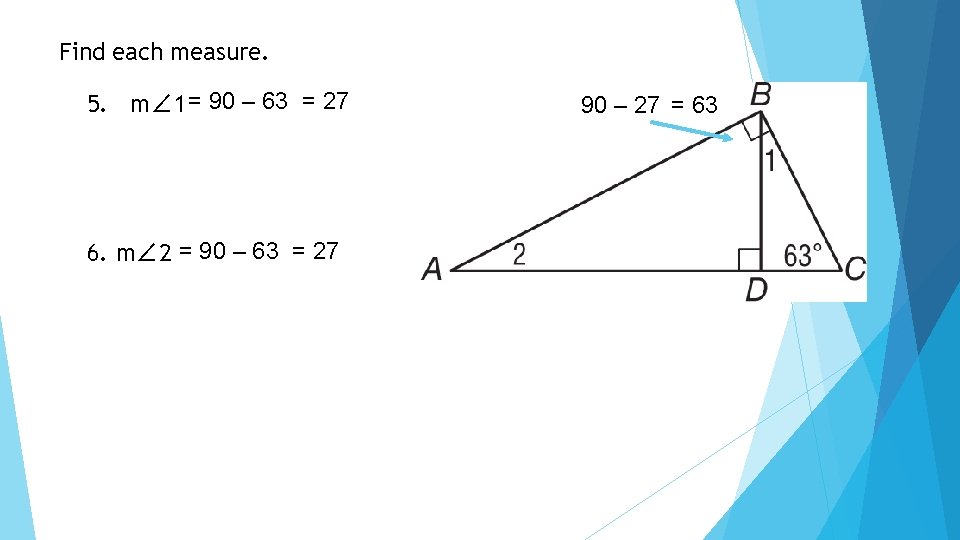



Content Standards G Co 12 Make Formal Geometric




Kpss Matematik Calameo Downloader



Angle And Trigonometric Functions 26 9 Sideway Output To



What Is The Ratio Of Sides Of A 30 75 75 Angle Triangle Without Sine Rule Quora
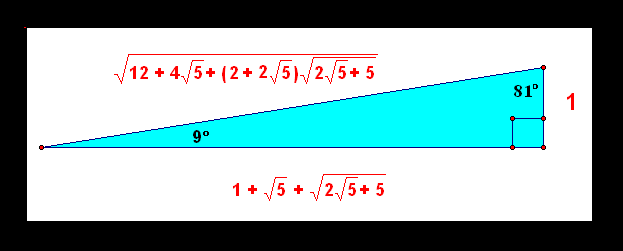



The 9 81 90 Triangle Robertlovespi Net




30 60 90 Ucgeni Ispat Youtube



2
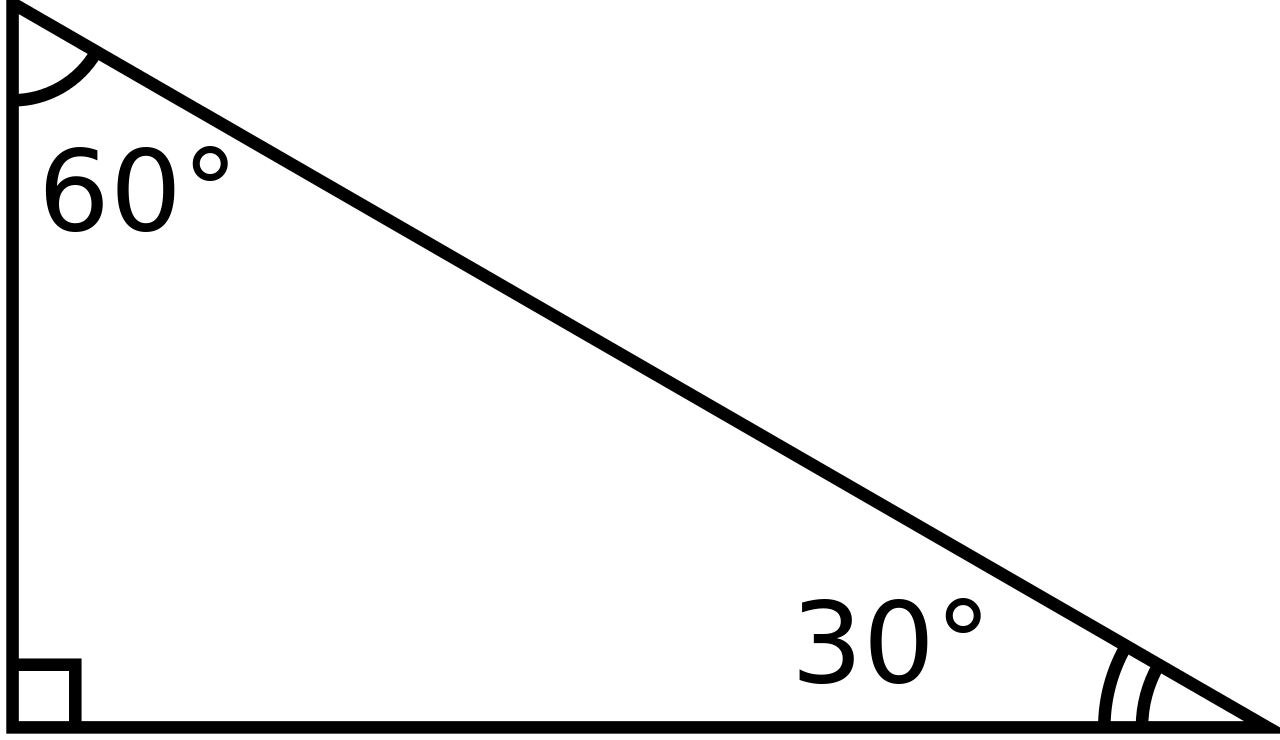



File 30 60 90 Triangle 2 Svg Wikimedia Commons
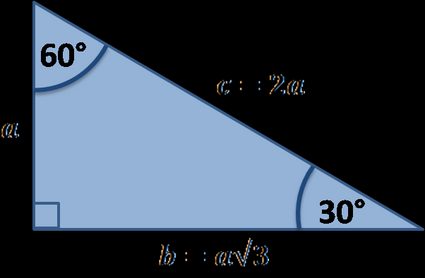



30 60 90 Triangle Calculator Formula Rules
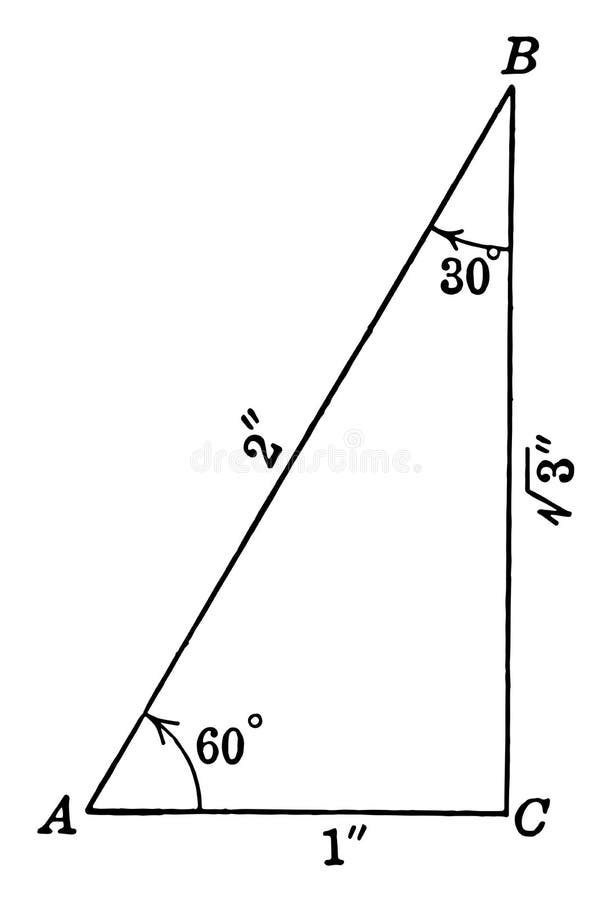



Triangle Degrees Stock Illustrations 248 Triangle Degrees Stock Illustrations Vectors Clipart Dreamstime




45 45 90 Ucgeni Ve Ozellikleri Not Bu




Dik Ucgen Vikipedi



30 60 90 Ucgeni Pisagormatik



Ozel Ucgenler Konu Anlatimi




High School Mathematics Lessons More Examples On 30 45 60 Degree Triangles



30 60 90 Triangle Calculator Formula Rules



45 45 90 Ucgeni Youtube




Cot 90 Kactir Iae News Site



70 90 Triangle Eylemmath




70 90 Ucgeni Hd Png Download Transparent Png Image Pngitem




Amal Triangle For Android Apk Download



Axisobject Wolfram Language Documentation




30 60 90 Triangle Calculator Formula Rules



45 45 90 Ucgeni Turleri Ve Ozellikleri



1



2




11 Maths Ideas In 21 Studying Math Math Methods Math Tricks



Vertical And Special Triangles Test 2 Course Geometry




Nereden Cikti Bu 30 60 90 Ucgeni 30 60 90 Ucgeni Ispati Youtube




En Hizli 45 60 90 Ucgeni



A 30 60 90 Triangle Math Central




En Hizli 30 60 90 Ucgeninin Ozelligi



2




Gmtri




Index Of Wp Content Uploads 18 05



The Easy Guide To The 30 60 90 Triangle



30 60 90 Triangles




En Hizli 30 60 90 Ucgeni Trigonometrik Oranlari



Triangle Sum Properties Objective Classify Triangles And Find




En Hizli 30 60 90 Ucgeni Kurali




Dik Ucgen 14 30 60 90 Ucgeni Ayrik Matematik Evde Egitim Psikoloji




Dik Ucgende 30 Un Karsisi 3 Ise 60 Ve 90 In Karsisi Ne Olur Eodev Com
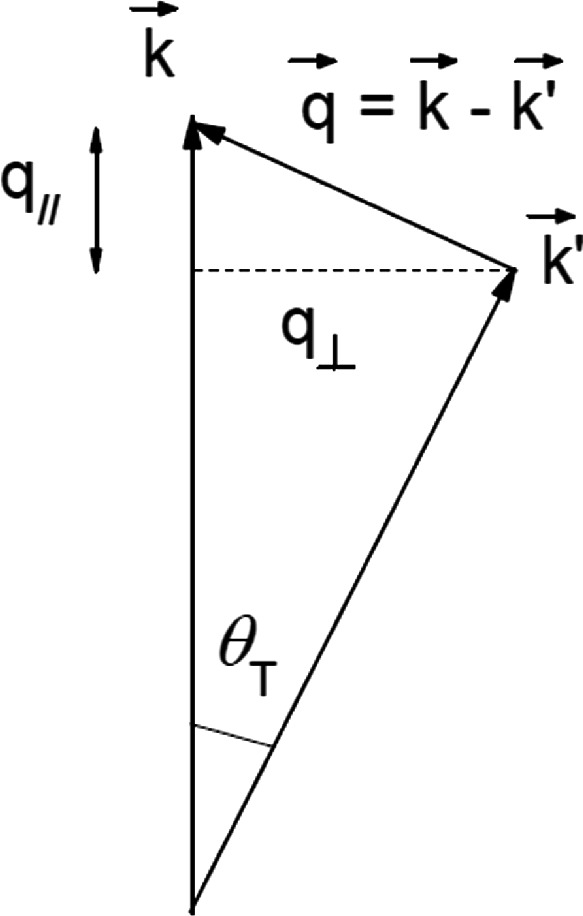



Photoelectron Energy Loss Spectroscopy A Versatile Tool For Material Science Springerlink



3



The 27 63 90 Triangle Robertlovespi Net



Oklid




30 60 90 Ucgeni Youtube



High School Geometry Complementary Angles



0 件のコメント:
コメントを投稿